[新しいコレクション] t=lambda x/l 827217-T=lambda x/l

This article is a summary of common equations and quantities in thermodynamics (see thermodynamic equations for more elaboration) SI units are used for absolute temperature, not Celsius or FahrenheitCopyright © Michael Richmond This work is licensed under a Creative Commons License Interference and the Twoslit Experiment This lecture is based on Sections 27No headers Imagine you have a sinusoidal traveling wave of the form (), only traveling to the left, incident from the right on a "fixed end" at \(x\) = 0The incident wave will go as \(\xi_{0} \sin 2 \pi(xc t) / \lambda\);

Lambda X Lambda X

T=lambda x/l

T=lambda x/l-Solution Let $V=\m{span}($ $e^{\lambda_1 x}$, $\cdots$, $e^{\lambda_n x})$, and define an operator $T\in \ca L(V)$ by $Tf=f'$(You should check $T\in \ca L(V)$) Then consider \Te^{\lambda_i x}=\lambda_ie^{\lambda_i x}\Hence $\lambda_i$ is an eigenvalue of $T$ with an corresponding eigenvector $e^{\lambda_i x}$Because the λ \lambda λ calculus is a programming language, we'll gradually develop the machinery to write out programs and encode data structures in this language To begin with, let us define True as choosing the first element and False as choosing the second element T = λ x λ y x F = λ x λ y y \begin{aligned} T &= \lambda x \lambda y x \\ F &= \lambda x \lambda y y \end

Understanding Lasso And Ridge Regression R Bloggers

Given T = Lambda X Lambda Y X F = Lambda X Lambda Y Y C = Lambda Plambda Q (p Q F) (same As K) (same As KI) (where F Is As Above) Find The Normal Forms Of A (C F F) B (CET) C (CTF) D (CTT) Does Anything About The Behavior Of These Lambda Terms Look Familiar?In words, the Memoryless Property of exponential distributions states that, given that you have already waited more than \(s\) units of time (\(X>s)\), the conditional probability that you will have to wait \(t\) more (\(X>ts\)) is equal to the unconditional probability you just have to wait more than \(t\) units of timeFor example, suppose you are waiting for the bus and the amount of timeNote that the expected value of a random variable is given by the first moment, ie, when \(r=1\)Also, the variance of a random variable is given the second central moment As with expected value and variance, the moments of a random variable are used to characterize the distribution of the random variable and to compare the distribution to that of other random variables

P = L / (LT), we have 0 < p < 1 and 1p = T / (LT), so P ( X=k XY=n ) = (n choose k) * p^k * (1p)^ (nk) We conclude that X given XY is distributed as a binomial with n = XY p = L / (LT) = Lambda / (Lambda Theta) Show moreBasically, it boils down to this, def f (_) # I'm the lambda _ t return 'o' def thegenerator () # I'm (f ( (yield x)) for x in l) for x in kvs yield f ( (yield x)) So when iterated over, thegenerator yields x (a member of kvs) and then the return value of f, which is always o, all in one iteration over kvsIn mathematics, particularly in functional analysis, the spectrum of a bounded linear operator (or, more generally, an unbounded linear operator) is a generalisation of the set of eigenvalues of a matrixSpecifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if − is not invertible, where I is the identity operator

In mathematics and economics, the envelope theorem is a major result about the differentiability properties of the value function of a parameterized optimization problem As we change parameters of the objective, the envelope theorem shows that, in a certain sense, changes in the optimizer of the objective do not contribute to the change in the objective functionSLAGTS may be used to solve one of the systems of equations where T is an n by n tridiagonal matrix, for x, following the factorization of (T lambda*I) as (T lambda*I) = P*L*U , by routine SLAGTFFormalized by John Tukey, the Tukey lambda distribution is a continuous, symmetric probability distribution defined in terms of its quantile function It is typically used to identify an appropriate distribution and not used in statistical models directly The Tukey lambda distribution has a single shape parameter, λ, and as with other probability distributions, it can be transformed with a location parameter, μ, and a scale parameter, σ Since the general form of probability distribution

Solved 5 Given T Lambda X Lambda Y X F Lambda X L Chegg Com

2

In mathematics and economics, the envelope theorem is a major result about the differentiability properties of the value function of a parameterized optimization problem As we change parameters of the objective, the envelope theorem shows that, in a certain sense, changes in the optimizer of the objective do not contribute to the change in the objective functionU(x,t) = X(x)T(t) \Rightarrow \frac{X''}{X} = \frac{T''}{T} = \lambda\\ X = C_1 cos(\sqrt{\lambda}x) C_2 sin(\sqrt{\lambda}x)\\X(0) = C_1 = 0\\X(L) = C_2 sin(\sqrt{\lambda}L) = 0 \Rightarrow \sqrt{\lambda}L = n\pi \forall n\geq 1 \Rightarrow \lambda = (\frac{n \pi}{L})^2\\We introduce an alternate yet a simple Fokas method (aka UTM) based approach for proving the interiorboundary Strichartz estimate for solutions of the initial boundary value problem (ibvp) for the Schrödinger equation posed on the right half line We utilize the solution representation formula obtained through the Fokas method and a few basic tools from the oscillatory integral theory

Announcing Lambda

Interference And The Two Slit Experiment

Provides information and entertainment resources, web site indexes, databases, virtual library links as well as links to its central library and branch library systemHow can I derive the formula $$\Delta \Phi = \frac{2\pi}{\lambda}\Delta x$$ for calculating the phase difference?SpaceX designs, manufactures and launches advanced rockets and spacecraft The company was founded in 02 to revolutionize space technology, with the ultimate goal of enabling people to live on other planets

Map Apply Applymap With The Lambda Function By Evelyn Li Medium

Introducing The New Lambda Function In Excel By Andrew Moss Codex Feb 21 Medium

462 Separation of variables;解得x=0，y=05，z=05，故 T = λ l g {\displaystyle T=\lambda {\sqrt {\frac {l}{g}}}} 只需用实验测出 λ {\displaystyle \lambda } 的值就可以了。The reflected wave should be flipped left to right and upside down, so change \(x\) to \(−x\) and put an overall minus sign on the displacement, to get \(\xi_{0

How To Transform Variables In A Pandas Dataframe By Zolzaya Luvsandorj Towards Data Science

Interference And The Two Slit Experiment

You also need to know the desired number of times the event is to occur, symbolized by x If you'd like to construct a complete probability distribution based on a value for $ \lambda $ and x, then go ahead and take a look at the Poisson Distribution Calculator It will calculate all the poisson probabilities from 0 to xStack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeSimilarly, define a left eigenvector as a row vector X_L satisfying X_LA=lambda_LX_L Taking the transpose of each side gives (X_LA)^(T)=lambda_LX_L^(T), which can be rewritten as

Amazon Com Go All Out Adult Lambda Lambda Lambda Tri Lambda Funny Triblend T Shirt Clothing

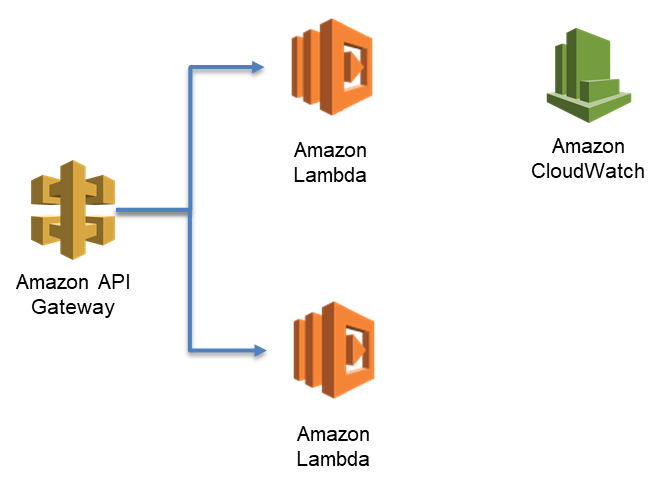
Investigating Spikes In Aws Lambda Function Concurrency Aws Compute Blog

Or, what exactly is particle velocity?461 Heat on an insulated wire;The \(\lambda\)calculus is, at heart, a simple notation for functions and application The main ideas are applying a function to an argument and forming functions by abstractionThe syntax of basic \(\lambda\)calculus is quite sparse, making it an elegant, focused notation for representing functions

Lambda Definition

Ppt Lisp Powerpoint Presentation Free Download Id

This article is a summary of common equations and quantities in thermodynamics (see thermodynamic equations for more elaboration) SI units are used for absolute temperature, not Celsius or FahrenheitAnswer to The temperature distribution ?A family of nested sets indexed by a single realvalued parameter $\lambda$, ie, a function $\mathcal{T}_\lambda \mathcal{X} \to 2^\mathcal{Y}$ such that if $\lambda \leq \lambda'$, then $\mathcal{T}_\lambda(x) \subseteq \mathcal{T}_{\lambda'}(x)$ There's almost always an automatic way of generating these nested sets from a given predictor

Solved 1 Point For The General Solution Of The Differen Chegg Com

Interior Point Methods

Adshelpatcfaharvardedu The ADS is operated by the Smithsonian Astrophysical Observatory under NASA Cooperative Agreement NNX16AC86AExplicit integration per vertex \(\vec{x}_i \leftarrow \vec{x}_i \delta t \, \lambda \Delta \vec{x}_i\) 0 iterations 10 iterations 100 iterations Uniform Laplace DiscretizationLet us recall that a partial differential equation or PDE is an equation containing the partial derivatives with respect to several independent variables

What Are Lambda Functions Lambda Function In Python

Lambda Definition

Where A is a generalized concave operator and \(\lambda>0\) is an eigenvalue In this article, we first state and prove a new fixed point theorem for a class of generalized concave operators Further, we establish some properties of positive solutions for the operator equation ()Here we do not assume the existence of upperlower solutions for the operator A, which is usually done in the(pretend You're All Excited Now And Want To Know More!) 6U(x,t) = X(x)T(t) \Rightarrow \frac{X''}{X} = \frac{T''}{T} = \lambda\\ X = C_1 cos(\sqrt{\lambda}x) C_2 sin(\sqrt{\lambda}x)\\X(0) = C_1 = 0\\X(L) = C_2 sin(\sqrt{\lambda}L) = 0 \Rightarrow \sqrt{\lambda}L = n\pi \forall n\geq 1 \Rightarrow \lambda = (\frac{n \pi}{L})^2\\

Lambda X L Ia Revelera T Elle Ce Que L On Ne Saurait Voir Regional It Toute L Information Sur Les Startups Et Les Tics En Region Wallonie Bruxelles

Wave Equations Springerlink

SoundCloud is a music and podcast streaming platform that lets you listen to millions of songs from around the world, or upload your own Start listening now!$$ \lambdak = A^T \lambdak1 Q Xk $$ $$ Pk Xk = A^T \left(I Pk1BR^{1} B' \right)^{1} Pk1 A Xk Q Xk $$ As above equation is satisfied for all \( Xk \), we get $$ Pk = A^T \left(I Pk1BR^{1} B' \right)^{1} Pk1 A Q $$ Equation above is called Riccati equation For discrete time, Riccati equation is more$\endgroup$ – copperhat Jan 4 at 10 $\begingroup$ @Chrystomath thanks for your suggestions I know that I need to check for a general $\lambda$ I started with $0$,

Vintage 90s Vintage Lambda Sigma Gamma Emerald Ball T Shirt Grailed

Lambda X Lambda X

Suppose that $ f $ and $ L $ are such that $ \sup _ {x \in X } \ L ( x) \ < \infty $ For each $ x \in X $, let $ L _ {p} ( x) = L ( f ^ { p 1 } ( x) ) \circ \dots L ( f ( x) ) \circ L ( x) $, where $ f ^ { r } $ denotes the $ r $ th iterate of $ f $ Define the (local) Lyapunov numbers and Lyapunov exponents by∂ L ∂ v x 1 = m v x 1 Δ t λ x Δ t = 0 v x 1 = − λ x m ∂ L ∂ v y 1 = m v y 1 Δ t λ y Δ t = 0 v y 1 = − λ y m ∂ L ∂ v z 1 = m v z 1 Δ t λ z Δ t = 0 v z 1 = − λ z m ∂ L ∂ v x 2 = m v x 2 Δ t λ x Δ t = 0 v x 2 = − λ x m ∂ L ∂ v y 2 = m v y 2 Δ t λ y Δ t = 0 v y 2 = − λ y m ∂ L ∂ v z 2 = m v z 2 Δ t λ z Δ t = 0 v z 2 = − λ z m e t c$\begingroup$ Surely something like ${h(t) \over g(t)\lambda}$ should feature above?

Church Encoding Wikipedia

Python Lambda Anonymous Function

NASAgov brings you the latest news, images and videos from America's space agency, pioneering the future in space exploration, scientific discovery and aeronautics researchSpaceX designs, manufactures and launches advanced rockets and spacecraft The company was founded in 02 to revolutionize space technology, with the ultimate goal of enabling people to live on other planetsFor problem 19, I think in the following way (I must admit that your solution is better) For F=C, then by 527, there is a basis of V to which T has an upper triangular matrix

Q Tbn And9gctqdkuyqz8kya2aveatfflj6xzfkdwvhvfxruhulyts Edsdocf Usqp Cau

Python Lambdas Explained With Examples Afternerd

Combining all this information together, we have \u_n(x,t) = \exp\left(k \frac{n^2\pi^2}{L^2}t\right)\sin\left(\frac{n\pi}{L}x \right)\ The equation we started from was linear and homogeneous, so we can superimpose the solutions for different values of \(n\), \u(x,t) = \sum_{n=1}^\infty c_n \exp\left(k \frac{n^2\pi^2}{L^2}t\right)\sin\left(\frac{n\pi}{L}x\right)\Sketch of the Proof of the Central Limit Theorem With the above result in mind, we can now sketch a proof of the Central Limit Theorem for bounded continuous random variables (see Theorem thm 947)The term \lambda (t) \dot x (t) acts as a Levenberg–Marquardt regularization of the continuous Newton dynamic associated with A, which makes (RN) a wellposed system The coefficient λ ( t) is allowed to tend to zero as t → ∞, which makes (RN) asymptotically close to the Newton continuous dynamic As a striking property, when λ ( t) does not converge too rapidly to zero as t → ∞ (with λ ( t) = e −t as the critical size), Attouch and Svaiter showed that each trajectory

Given That Y A Sin 2pi Lambda Ct X Where Y

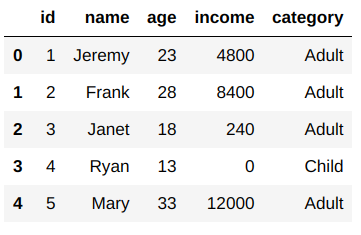
What Are Lambda Functions Lambda Function In Python

On a relative note, why does the particle velocity have an upwards direction when the wave travels below the xaxis?Ridge regression introduction¶ This notebook is the first of a series exploring regularization for linear regression, and in particular ridge and lasso regression We will focus here on ridge regression with some notes on the background theory and mathematical derivations that are useful to understand the concepts Then, the algorithm is implemented in Python numpy( x , t ) along an insulated metal rod of length L is described by the differential equation ?

Purdue Debris H X Lambda Chi Alpha Founded At Boston University November 2 1909 X Psr Zeta Chapter Established At Purdue December 11 1915 Fifty Five Chapters Dr R H Carr Faculty

Www Utdallas Edu Gupta Courses Apl Lambda Pdf

29 votes, 335 comments Today is Day and the final weekend puzzle for the year Hold on to your butts and let's get hype!Basically, it boils down to this, def f (_) # I'm the lambda _ t return 'o' def thegenerator () # I'm (f ( (yield x)) for x in l) for x in kvs yield f ( (yield x)) So when iterated over, thegenerator yields x (a member of kvs) and then the return value of f, which is always o, all in one iteration over kvsOverview An important extension to the basic Poisson Process with rate \(\lambda\) is to consider that each arrival may be categorized according to a certain type If we let \(K\) be the total number of types, we might build a model in which the types are determined probabilistically according to a set of type probabilities (\(p_1,\ldots,p_K\), \(\sum_{i=1}^K p_i = 1\))

Z Z A X Varepsilon L Mathcal X L X Z Mathbf L Lambda Zeta A X C Zeta A X Z L A Zeta X 0 T Lambda Varepsilon X Z

Lambda Definition

Lambda Definition

Q Tbn And9gcrmq1jd1ddfbkljcvaugnwtuqibldl0wiwxfnljm22prkbmipgg Usqp Cau

Given That The Eigenvalue Problem X X Lambda X X Chegg Com

Python Tutorial Lambda Operator Filter Reduce And Map

Apply And Lambda Usage In Pandas Learn These To Master Pandas By Rahul Agarwal Towards Data Science

Solved 5 Given T Lambda X Lambda Y X F Lambda X L Chegg Com

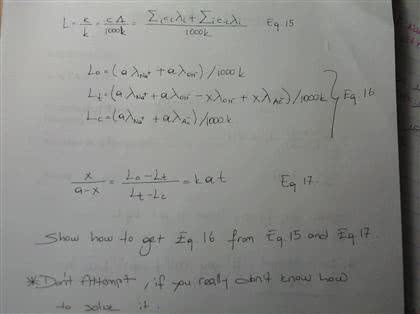
Oneclass L K L Ca 1000k C1 Lambda 1 C1 Lambda 1 1000k Eq 15 L0 A Lambda A Lambda 10

Why Doesn T Lambda Theta Below Have To Divide By M Andrew Ng S Machine Learning Course Mlquestions

The Lambda Calculus For Developers Simon Holywell

Understanding Lasso And Ridge Regression R Bloggers

Announcing Lambda

2

Solved A I Find The General Solution To The Ode Ii Sh Chegg Com

Solved Consider The Lagrangian L E Lambda T M 2 X 2 Ob Chegg Com

Vtg Pi Lambda Phi Champion Reverse Weave Sweatshirt Crewneck Xl 90s Ya Throwback Vault

Lambda X S A Linkedin

Cs55 Foundation In Programming Languages Lecture 1 Overview Ppt Video Online Download

Full Metal Panic Lambda Driver T Shirt Black Xl Anime Toy Hobbysearch Anime Goods Store

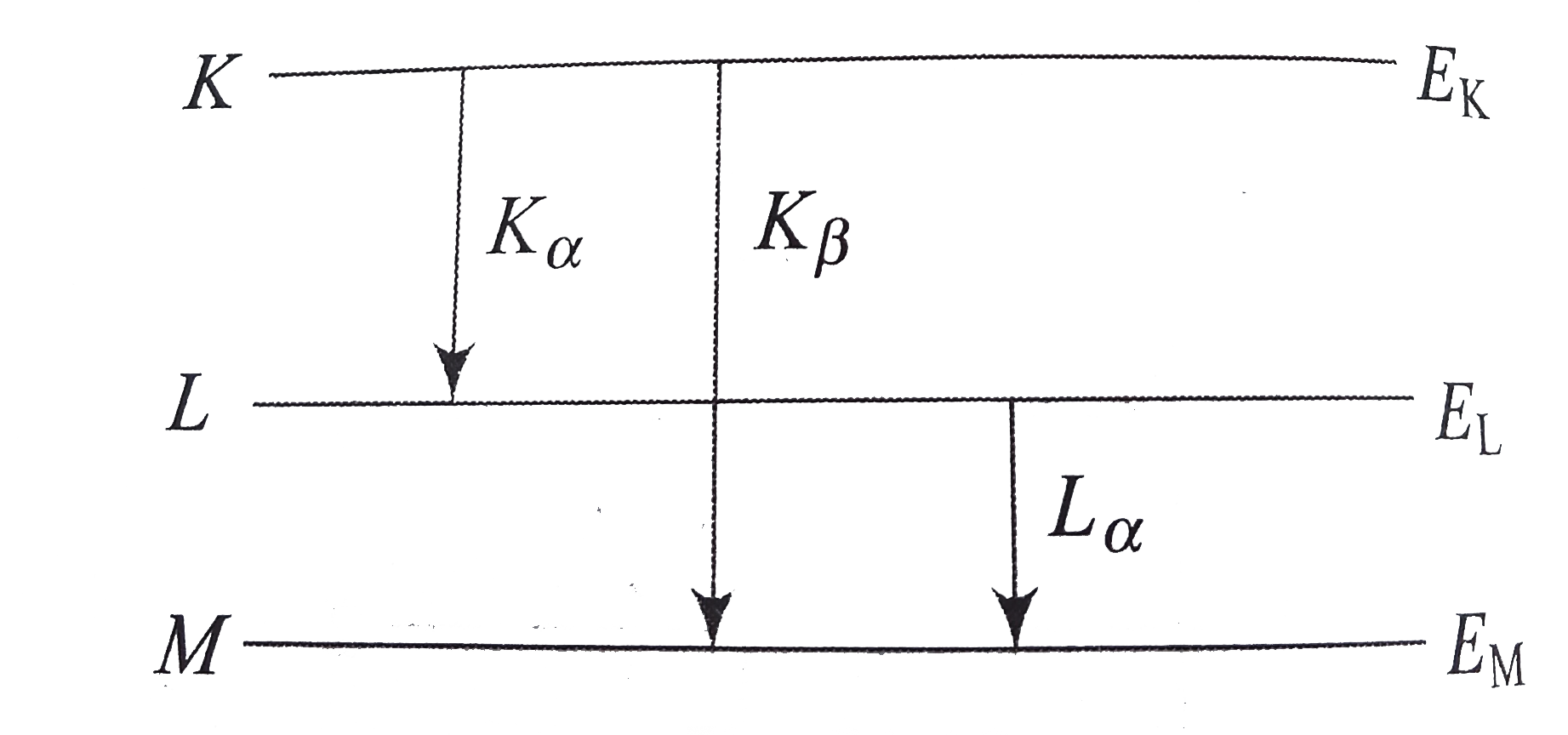
Let Lambda Alpha Lambda Beta And Lambda Alpha Denote T

Using Container Images To Run Pytorch Models In Aws Lambda Aws Machine Learning Blog

Nerds Lambda Lambda Lambda Frat Shirt Xl Revenge Of The Nerds Movie Fraternity Lambda Lambda Lambda Length 30 Pit To Pit 23 Nerd Frat Lambda

Convolution Interval

Mathematics Probability Distributions Set 2 Exponential Distribution Geeksforgeeks

Lambda Probe O2 Oxygen Sensor Fit For Seat Alhambra Exeo Ibiza Altea Xl Leon Toledo Cordoba 1 4 2 0 T 02 12 Exhaust Gas Oxygen Sensor Aliexpress

What Is A Lambda Function Stack Overflow

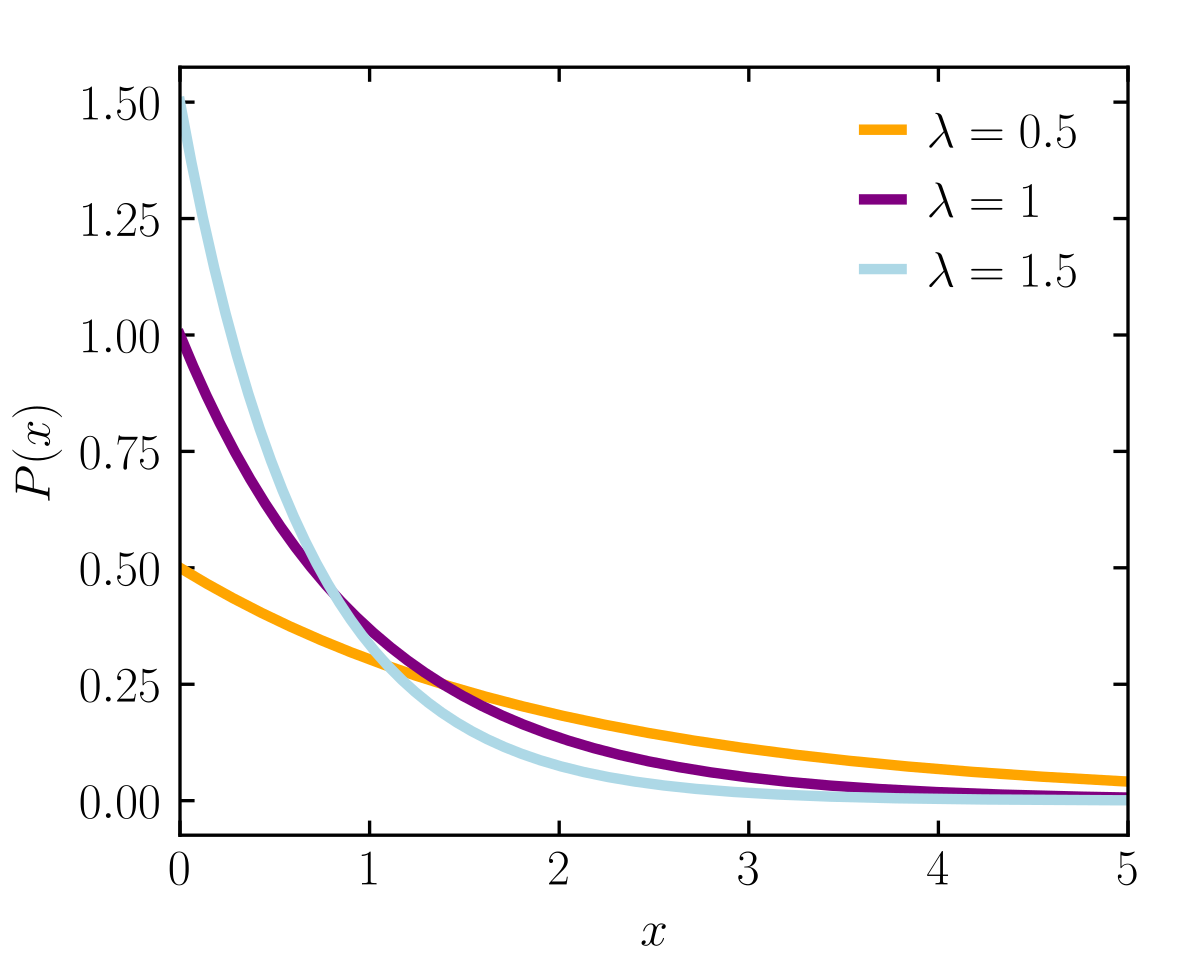
Exponential Distribution Wikipedia

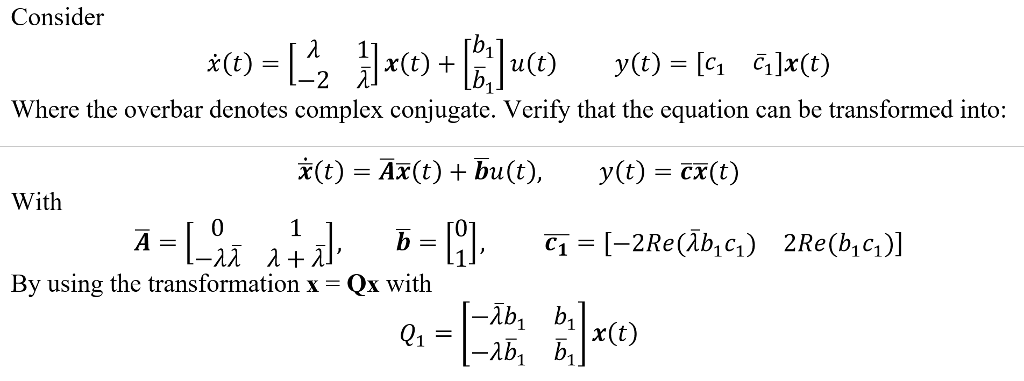
Solved Consider X T Lambda 1 2 Lambda X T B 1 B Chegg Com

5 Given T Lambda X Lambda Y X F Lambda X L Chegg Com

Exponential Distribution Wikipedia

Peginterferon Lambda For The Treatment Of Outpatients With Covid 19 A Phase 2 Placebo Controlled Randomised Trial The Lancet Respiratory Medicine

Solved I Don T Understand How This Lambda Was Found I Th Chegg Com

Search Q N Lambda 3d D Sin Theta Tbm Isch

Find Coordinates Of Mass Center Of A Non Uniform Rod Of Length L W

Vintage 90s Lambda Chi Alpha Headbangers Ball 1993 Party Distressed T Shirt Xl Ebay

Efficient Upper And Lower Bounds For Global Mixed Integer Optimal Control Springerlink

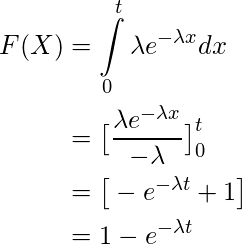
Mathematics Probability Distributions Set 2 Exponential Distribution Geeksforgeeks

Vintage 90s Vintage Lambda Sigma Gamma Emerald Ball T Shirt Grailed

Lambda Lambda Lambda T Shirt That Funny Shirt Xl Kelly Green Buy Online In Isle Of Man At Isleofman Desertcart Com Productid

F X Int A X F T Lambda Dt Is Absolutely Continuous For All F In L 1 Lambda Mathematics Stack Exchange

2

Python Lambda Anonymous Function

Solved U X T Summation N 1 Infinity B N S In N Pi X Chegg Com

Young S Double Slit Equation Video Khan Academy

Lambda X S A Linkedin

Lambda Functions As Targets For Application Load Balancers Networking Content Delivery

2

Q Tbn And9gcqhrldzch5pw8x Uk0jggaxir7oboufk5znrsm2rr3pilfijadr Usqp Cau

Announcing Lambda

Interference And The Two Slit Experiment

Mike Kornhauser Interference And Diffraction

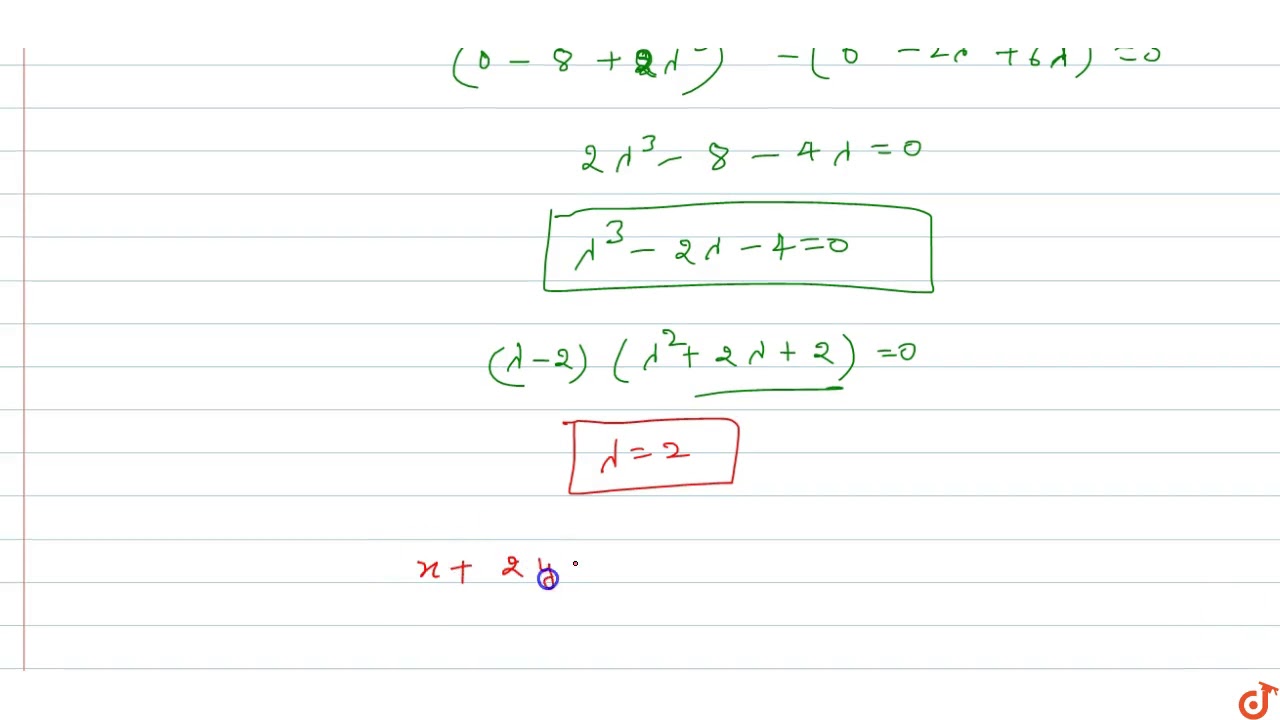
Find The Real Values Of Lambda For Which The Following System Of Linear Equations Has Non Triv Youtube

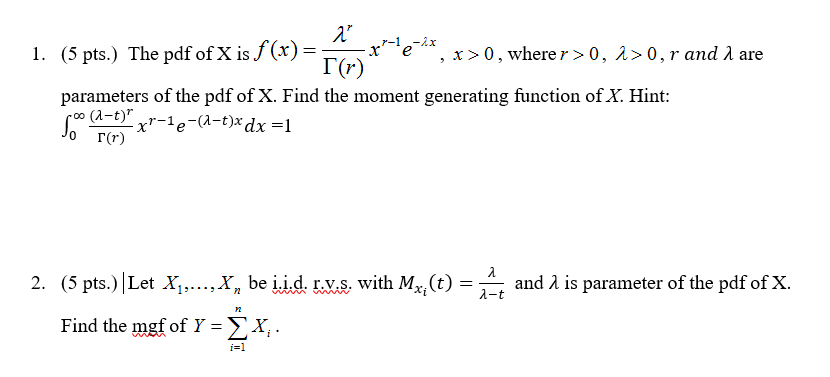
Solved The Pdf Of X Is F X Lambda Gamma R X R 1 E L Chegg Com

Lambda Lifting Wikipedia

157 Questions With Answers In Lambda Science Topic

Macvim Thinks I Have Unmatching Parentheses Until I Place Cursor Over Each Parenthesis Vi And Vim Stack Exchange

Random Trajectory On A Sphere Chebfun

Python Lambda Anonymous Function

Solved In Your Answers Below For The Variable L Type The Chegg Com

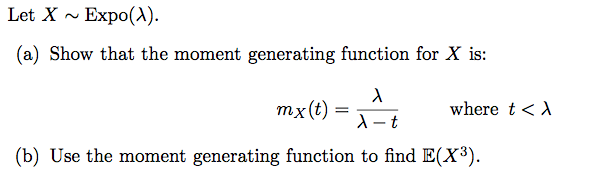
Solved Let X Expo Lambda A Show That The Moment Gen Chegg Com

Ppt Lisp Powerpoint Presentation Free Download Id

Http Statweb Stanford Edu Jtaylo Courses Stats116 Assignments Solution9 Pdf

2

Announcing Lambda

Interference And The Two Slit Experiment

What Are Lambda Functions Lambda Function In Python

菜鸟大反攻tri Lambda Xl 黑色t 恤02 垃圾食品标签 Ebay

Vintage 90 S Georgetown College Lambda Chi Alpha Long Sleeve T Shirt Xl Hanes Ebay

Wave Equations Springerlink

Vintage 90s Vintage Lambda Sigma Gamma Emerald Ball T Shirt Grailed

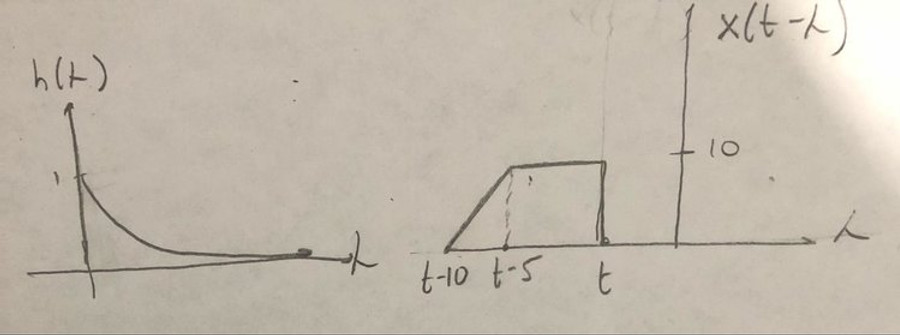
Convolution Interval

Exponential Distribution Wikipedia

Wave Equations Springerlink

2

Hw 4

Incoming Term: t=lambda x/l,